本文是对Real-Time Rendering一书中第18章Graphics Hardware的读书笔记。这一节比较短,讲的是透视正确的插值。
18.2 透视正确的插值(Perspective-Correct Interpolation)
透视正确的插值很重要,因为它决定了渲染图元上的纹理渲染效果看起来是否正确。我们知道,每个顶点v在经过投影变换后得到新的坐标\(p = (p_x, p_x, p_z, 1)\)。在DirectX里,\(p_z\)的范围就是[0, 1],在OpenGL里是[-1, 1]。但是,我们在上一节也提到过,缓存里面的深度精度为b个bits的话,深度缓存的范围就是\([0, 2^b - 1]\),这就需要我们对\(p_z\)进行一个简单的平移和放缩操作。而且,每个订单可能会有一系列顶点属性,例如纹理坐标和颜色等,这些属性也需要进行插值。
三角形之间的屏幕坐标\((p_x, p_y, p_z)\)可以直接使用线性插值来得到。在真正的实践中,这通常是通过计算梯度来实现的:\(\frac{\delta{z}}{\delta{x}}\)以及\(\frac{\delta{z}}{\delta{y}}\)。这些梯度表示两个相邻像素在x和y方向上\(p_z\)是如何变化的。然而,颜色特别是纹理坐标是不能直接使用线性插值的。下图就是一个对比效果。左图是直接对纹理坐标进行线性插值得到的错误结果,右图是使用了透视正确的插值。出现左图这种效果的原因是,直接线性插值的话是在屏幕空间的插值,因此就不会有正确的透视效果,可以看到左图里面格子的间距都是一样的,而没有任何透视关系。

为了解决这个问题,Heckbert、Moreton[1]和Blinn[2]指出\(\frac{1}{w}\)和\((\frac{u}{w}, \frac{v}{w})\)是可以线性插值的,其中w就是投影空间下顶点的w分量值。也就是说,我们可以对\(\frac{1}{w}\)和\((\frac{u}{w}, \frac{v}{w})\)进行正常的线性插值,然后再使用\((\frac{u}{w}, \frac{v}{w})/(\frac{1}{w}) = (u, v)\)来得到正确的纹理坐标。这种插值方法被称为双曲线插值(hyperbolic interpolation),也被称为有理线性插值(rational linear interpolation),因为分子和分母被分别线性插值了。
我们来举个栗子。假设现在需要对一个三角形进行光栅化,并且每个顶点为:
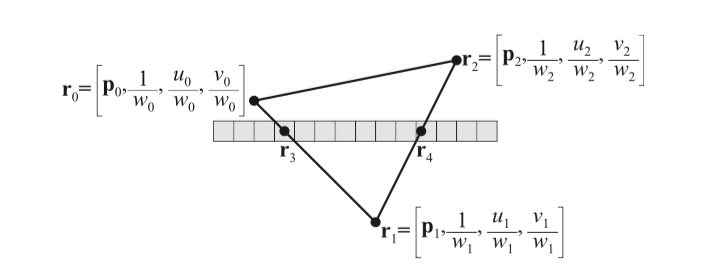
\[\boldsymbol{r}_i = [\boldsymbol{p}_i, \frac{1}{w_i}, \frac{u_i}{w_i}, \frac{v_i}{w_i}]\]其中,\(\boldsymbol{p}_i\)是经过投影变换和透视除法后的顶点坐标,\(w_i\)是投影空间中的w分量,\((u_i, v_i)\)是该顶点的纹理坐标。如下图所示,硬件一般会使用扫描线方法。为了找到图示灰色水平扫描线上的某个像素的坐标,我们首先会对\(\boldsymbol{r}_0\)和\(\boldsymbol{r}_1\)线性插值得到\(\boldsymbol{r}_3\),然后再对\(\boldsymbol{r}_2\)和\(\boldsymbol{r}_1\)线性插值得到\(\boldsymbol{r}_4\),最后对\(\boldsymbol{r}_3\)和\(\boldsymbol{r}_4\)线性插值得到该像素的\(\boldsymbol{r}\)。这样插值得到的\(\boldsymbol{p}\)值,即像素坐标是正确的。而纹理插值结果\((u/w, v/w)\)还需要乘以插值后的\(w\)值来得到最终的\((u, v)\)。
这种扫描线的插值实现只是一种选择。另一个可能的实现是计算梯度来得到纹理插值。这里不再赘述了。
关于透视正确的插值的深度讨论可以参见Blinn的三篇文章[2, 3, 4]。作者还提到,在现代GPU的实现中,edge function[5] 经常会被用于判断一个采样点是否在某个三角形内。一个edge function其实就是一个简单的2D直线等式方程。而作为一个有趣的附加作用,透视正确的插值也可以通过使用evaluated edge functions[6]来得到。
笔者注
这小节讲得比较简要,但关键的地方作者都提到了。关于数学部分的推导可以参考《Mathematics for 3D game programming and computer graphics》一书的5.4节,Perspective-Correct Interpolation。
[1] Heckbert, Paul S., and Henry P. Moreton, “Interpolation for Polygon Texture Mapping and Shading,” State of the Art in Computer Graphics: Visualization and Modeling, Springer-Verlag, pp. 101–111, 1991. Cited on p. 838
[2] Blinn, Jim, “Hyperbolic Interpolation,” IEEE Computer Graphics and Applica- tions, vol. 12, no. 4, pp. 89–94, July 1992. Also collected in [105]. Cited on p. 838, 840
[3] Blinn, Jim, Jim Blinn’s Corner: A Trip Down the Graphics Pipeline, Morgan Kaufmann, 1996. Cited on p. 27, 662, 663, 840, 927
[4] Blinn, Jim, “W Pleasure, W Fun,” IEEE Computer Graphics and Applications, vol. 18, no. 3, pp. 78–82, May/June 1998. Also collected in [110], Chapter 10. Cited on p. 840
[5] Pineda, Juan, “A Parallel Algorithm for Polygon Rasterization,” Computer Graphics (SIGGRAPH ’88 Proceedings), pp. 17–20, August 1988. Cited on p. 840
[6] McCool, Michael D., Chris Wales, and Kevin Moule, “Incremental and Hierarchi- cal Hilbert Order Edge Equation Polygon Rasterization,” Graphics Hardware, pp. 65–72, 2001. Cited on p. 840